1 概要

ある変数と別の変数に関連性があるかを調べるために、相関係数という値を調べます。相関係数は測定の単位に依存せず、「-1～1」の範囲で表され、正であれば、一方の変数が大きくなるにつれてもう一方の変数も増加する右肩上がりの関係になり、絶対値が 1 に近づく程その関係が強いことを表しています。また、負は正の逆の関係になります。相関係数を調べる代表的な手法として、「ピアソンの積率相関係数」と「スピアマンの順位相関係数」があり、今回はどのような場面でどちらを採用すれば良いのかを紹介します。

2 相関係数

2 つ以上の変数が存在する場合に、ある変数 (𝑥)が変化した時に、他方の変数 (𝑦)もその変化に応じて変化する関係のことを相関関係といいます。そして、この関係を統計的に分析することを相関分析と言います。相関関係は 2 種類のデータがお互いに影響を与え合っている相互関連性のことであるので、因果関係ではないことに注意しましょう。

2.1 ピアソンの積率相関係数

一般的な相関分析ではこちらのピアソンの積率相関係数を指しており、特徴として対象とする 2 変数が正規分布に従っていることを仮定しています。ピアソンの積率相関係数は以下の式のように 2 変数間の標本共分散をそれぞれの標本分散の平方根で割ったものとして計算されますが、これは 2 変量正規分布の相関パラメータを推定し、 2 変数の間の線形な関連性を算出したものになります。注意しなければならないのは、変数に順序尺度ある場合や非線形のような関係には効果を発揮することが出来ない点です。このような場合にはスピアマンの順位和相関係数を用いるのが適切であるとされています。

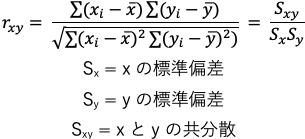
2.2 スピアマンの順位相関係数

データの母集団が正規分布に従わないようなデータ (ノンパラメトリック)である場合はスピアマンの順位相関係数を用いることが推奨されています。スピアマンの順位相関係数では各データの値をデータ内の順位に変換し以下のように計算しています。 2 つの変数の分布について仮定していないため、Spearmanの順位相関係数は外れ値の影響を受けにくく、順序尺度にも使用できるといった利点があります。

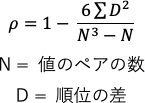
3 まとめ

ピアソンの積率相関係数では各データが正規分布に沿ったデータであるということが重要になります。ピアソンの積率相関係数では正規分布に従っていることから、信頼区間を推定することが可能です。しかし、ピアソンの積率相関係数は「外れ値」に弱く、 1 つでもデータがかけ離れたプロットにある場合にはその外れ値を除外しないと、相関係数がその外れ値に引っ張られてしまい、実際には相関係数が低いにも関わらず高く出てしまう場合があります。一方で、スピアマンの順位相関係数では、ピアソンの積率相関係数と違い、生データではなく順位データであるため、外れ値などには頑健性があるものの、それぞれの変数間の情報、すなわち各データの変化量情報が失われてしまいます。これらのことから、使い分けは以下の表のような 2変量の組み合わせパターンとなります。

  順序尺度 ノンパラメトリック パラメトリック
順序尺度 順位相関係数 順位相関係数 順位相関係数
ノンパラメトリック – 順位相関係数 順位相関係数
パラメトリック – – 積率相関係数

どちらの相関係数も単調な関係性を評価するものであるため、因果関係を推論することは避けるべきであり、相関関係は一致度の分析には適しません。相関は非線形または非単調な関係を適切に表現できないため、相関係数を算出する前に散布図を作成することが推奨されます。

4 参考文献

  • 川瀬 雅也, 生物学のための統計学入門，化学同人 2009.
  • 奥田 千恵子, 医薬研究者の視点からみた　道具としての統計学,金芳堂 2011
  • Schober P, Boer C, Schwarte LA. Correlation Coefficients: Appropriate Use and Interpretation. ANESTHESIA & ANALGESIA. 2018; 126 (5): 1763-68 DOI: 10.1213/ANE.0000000000002864
  • 椎名 乾平, 相関係数の起源と多様な解釈,心理学評論. 2016; 59 (4): 415-44 DOI:https://doi.org/10.24602/sjpr.59.4_415

ヒト臨床試験 (ヒト試験) で得られる結果は、様々な誤差を含んでいます。この誤差を小さくすることで介入効果を増大させることができます。オルトメディコは、多分野の専門家を有するため、様々なアプローチにより誤差を最小化する試験運営が可能です。引き続き、皆様にご満足いただけるような高品質なヒト試験を提供させていただきますので、今後ともどうぞ宜しくお願い申し上げます。

この記事をPDFでダウンロードする

★問い合わせ★